The main aspect of a simulation is the analysis of the operational sequence of processes during their dynamic progression. The processes to be analyzed are instantiated (started or generated) at start events. In agreement with their respective areas of application, users must be able to decide when and how often processes should be instantiated. In addition, the user needs to be able to prioritize processes so that urgent processes can be taken into account, for example.

ARIS Method prioritizes tasks by specifying the Priority attribute (Simulation attribute type group) for start events, and all processes instantiated at the corresponding start event retain this priority.

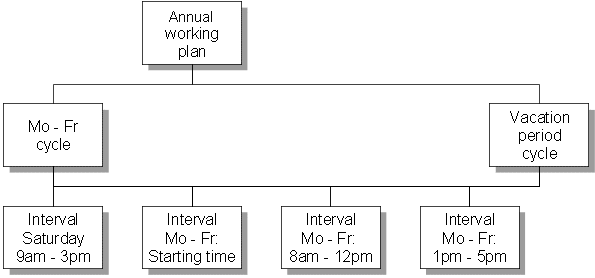
The requirement described is met by the process instantiation model. This model is developed as a multi-level object model. The Instantiation interval object is at the lowest level. Such an interval contains the Relative interval start, Interval duration, Number of process instances, Distribution, Repeat in cycles, and Period attributes. An interval duration of 0 is permitted in order to express a certain point in time. While intervals describe shorter periods of time, process instantiation cycles are used to repeat an ever recurring sequence of intervals. For example, a day can be modeled by four different intervals, which are repeated as a cycle for the entire simulation time period (for example, a week). But it is also possible to divide the simulation time period into several cycles (for example, work days and weekends), each of which may contain different intervals. A process instantiation plan may contain one or more cycles. The following example explains the object model more clearly:

A process model exists as an EPC with a start event. The following assumptions apply for this process: On weekdays (Mon - Fri), 50 processes are started at 8.00 a.m. at the beginning of the working day. From 8:00 am to 12:00 noon as well as from 1:00 p.m. to 5:00 p.m., 20 processes are started in equal distribution; from 12:00 noon to 1:00 p.m. and outside of work hours, no processes will be started. On Saturday, 60 processes will be started in a triangular distribution from 9:00 a.m. to 3:00 p.m. Generally, no processes are started on Sundays. This weekly rhythm applies from January to December, except during the vacation period from July to August. During this period, no one works on Saturdays.

Based on the example described above we can generate the following model: