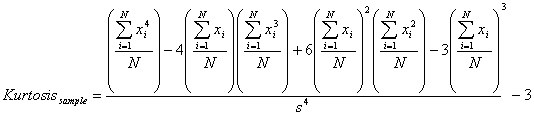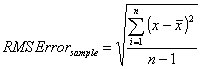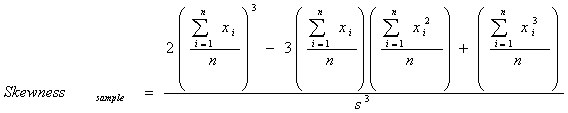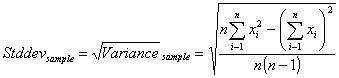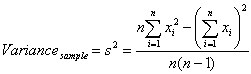This function returns the 1st value of the unsorted population.

value_exp can be an expression of any SQL data type.

Example:

The function will return 5 from the above table, because 5 is the 1st value in the population.

Returns the Kth largest item indicated by k_numeric_exp in the population of numeric_exp.

For any K supplied, there will be at most K-1 items that are larger. If you ask for K=1, then zero elements are larger; therefore you must have the largest item. If you ask for K=20, then up to 19 elements can be larger.

numeric_exp must be a number, or a numeric expression.

k_numeric_exp must be a number, or a numeric expression.

Examples:

For the numeric column L with values 1,2,3,2,5,6,7,8,9,4,2,22:

The result is the same as sorting the list (descending, ascending for KTHSMALLEST) and then picking the Kth element from the list. But it is much faster than sorting.

Returns the Kth smallest item indicated by k_numeric_exp in the population of numeric_exp.

For any K supplied, there will be at most K-1 items that are smaller. If you ask for K=N (where N is the total number of things in the list), then zero elements are larger; therefore you must have the smallest item. If you ask for K=20, then up to 19 elements can be smaller.

numeric_exp must be a number, or a numeric expression.

k_numeric_exp must be a number, or a numeric expression.

Examples:

For the numeric column L with values 1,2,3,2,5,6,7,8,9,4,2,22:

This may seem surprising, but if you sorted the list, it would look like this: 1,2,2,2,3,4,5,6,7,8,9,22 and so the 2nd, 3rd and 4th smallest elements of the list are all 2.

The result is the same as sorting the list (ascending, descending for KTHLARGEST) and then picking the Kth element from the list. But it is much faster than sorting.

KURTOSIS returns the Kurtosis of the population of numeric_exp, where numeric_exp is a sampling of a larger population. KURTOSISP returns the kurtosis of the whole population.

Kurtosis is used in distribution analysis to describe how big the tails are for a distribution. Kurtosis indicates the likelihood of an event far away from the average. Kurtosis is based on the size of a distribution's tails. A distribution with approximately the same kurtosis as the normal distribution is called mesokurtic (meaning medium-curved). The mesokurtic kurtosis of a normal distribution is 0. If a distribution is short and flat with small tails, it is described as platykurtic (flat-curved). For a platykurtic distribution, individual observations are spread out fairly uniformly across their range. If a distribution is tall and slender with relatively large tails it is spoken of as leptokurtic (slender-curved). For a leptokurtic distribution, observations tend to cluster densely about some particular point in the range.

KURTOSIS formula:

where s (sigma for KURTOSISP) is the standard deviation of the sample (or the whole population for KURTOSISP). Subtract 3 because the kurtosis of the normal distribution is 3 (without the subtraction). By subtracting 3, the direction of the kurtosis can be seen by examining its sign. Kurtosis ranges from -2 (highly platykurtic) to 0 (mesokurtic) to +infinity (highly leptokurtic).

This function returns the nth value of the unsorted population of n

value_exp can be an expression of any SQL data type.

Example:

The function will return 30 from the above example, because it's the last (6th in this case) value in the population.

This function returns the median value of the population of numeric_exp.

numeric_exp must be a number, or a numeric expression.

The median is used to indicate the center of a given population at the point where the distribution of scores is divided in half. Given a population of "n":

For example, for a resultset of four values, the median would be the average (or mean) of values 2 and 3. Take the following values:

The median of the above example is 25.

If the number of data points is less than QUANTILE_ESTIMATION_THRESHHOLD, then the calculation for a median or quantile will proceed as follows:

If the number of data points is greater than or equal to QUANTILE_ESTIMATION_THRESHHOLD, the quantile position is estimated by the linear time selection algorithm "Randomized-Select" as described in introduction to Algorithms by Cormen,Leiserson, and Rivest, p. 187.

This function returns the middle value of the unsorted population of value_exp.

value_exp can be an expression of any SQL data type.

Middle will return the (n+1)/2'th value, performing integer division.

Examples:

The above example would return 2, because it is the 3rd value in the population ((6+1)/2 = 3.5 ~=3).

The above example would return 2, because it is the 3rd value in the population ((5+1)/2 = 3).

This function returns the mode of the population of value_exp.

value_exp can be an expression of any SQL data type.

The mode is used to indicate the location of the center of a population. The mode is not an indicator of the frequency of the score that occurs most often, but rather the actual value of the score.

Examples:

With a resultset of the following six values (v1, v2, v3, v4, v5, v6), the mode would be the 25, because it occurs the most number of times:

Returns the count of unique values, if any, that makes the population of value_exp multi modal.

value_exp can be an expression of any SQL data type.

This function returns the number of unique values that cause a population to be multimodal. In other words, this function only returns results if the population is multimodal. If the population is not multimodal, this function returns 0.

Examples:

With a resultset of the following six values (v1, v2, v3, v4, v5, v6), the multimodalcount would be the 0, because the population is not multimodal (there is a single mode, 25):

In the following example, the multimodalcount would be 2, because the population is multimodal, and the number of unique values that make the population multimodal is two (8 and 25).

This function returns the number of times the mode occurs in the population of value_exp (even in multi-modal populations).

Examples:

With a resultset of the following six values (v1, v2, v3, v4, v5, v6), the multimodaloccur would be the 3, because the mode, 25, occurs three times:

In the following example, the multimodaloccur would be 2, because there is more than one value that repeats at the highest frequency (both 25 and 8), and they both repeat twice:

Returns the quantile specified by Q_numeric_exp for the population of numeric_exp.

numeric_exp must be a number, or a numeric expression.

Q_numeric_exp (the quantile to compute) must be a floating point number strictly between 0 and 1.

The quantile of a distribution of values is a number xp such that a given proportion of the population values are less than or equal to xp. For example, the 0.75 quantile (also referred to as the 75th percentile or upper quartile) of a variable is a value xp such that 75% of the values of the variable fall below that value. The 0.5 quantile is the median.

If the number of data points is less than QUANTILE_ESTIMATION_THRESHHOLD, then the calculation for a median or quantile will proceed as follows:

If the number of data points is greater than or equal to QUANTILE_ESTIMATION_THRESHHOLD, the quantile position is estimated by the linear time selection algorithm "Randomized-Select" as described in introduction to Algorithms by Cormen,Leiserson, and Rivest, p. 187.

This function returns the First Quartile for the population numeric_exp.

numeric_exp must be a number, or a numeric expression.

QUARTILE1 is the 0.25 quantile. It is used frequently in other calculations such as the inter-quartile range, the quartile deviation, and the quartile variation coefficient.

Returns the Third Quartile for the population of numeric_exp.

numeric_exp must be a number, or a numeric expression.

QUARTILE3 is the 0.75 quantile. It is used frequently in other calculations such as the inter-quartile range, the quartile deviation, and the quartile variation coefficient.

Returns the range of the population of numeric_exp.

numeric_exp must be a number, or a numeric expression.

The range is the simplest measure of the spread or dispersion of a data set. The range is the difference between the highest and lowest values in a Set. The range reflects information about extreme values but not necessarily about typical values. Only when the range is narrow (meaning that there are no outliers) does it tell us about typical values in the data. The higher the range, the greater the amount of variation in a data set.

Range = Max - Min

Where:

Max = Highest observed value in the data set

Min = Lowest observed value in the data set

RMSERROR returns the RMS error of the population of numeric_exp, where numeric_exp is a sample of a larger population. Use RMSERRORP to return the RMS error of a whole population.

numeric_exp must be a number, or a numeric expression.

To calculate the root mean squared error, the individual errors are squared, added together, dividing by the number of individual errors, and then the square root is taken. This gives a single number that summarizes the overall error.

SKEWNESS returns the skewness of the population of numeric_exp, where numeric_exp is a sample of a larger population. Use SKEWNESSP to retrieve the sample of the whole population.

numeric_exp should be a numeric column or a numeric expression.

A set is skewed if one of its tails is longer than the other. A set has a positive skew if it has a long tail in the positive direction. A set has a negative skew if it has a long tail in the negative direction. A set is perfectly symmetrical if it has no skew. Though negatively skewed sets do occur, sets with positive skews are more common than sets with negative skews. Skew can be calculated as:

As a general rule, the mean is larger than the median in positively skewed sets and less than the median in negatively skewed sets. The standard deviation is not a good measure of spread in highly skewed distributions and should be augmented in those cases by the semi-interquartile range. Skew is sometimes called the third moment of a set. A set with a skew of zero is one that is not lopsided in either direction. A set with a skewness of 1 or more is highly skewed. A set with a skewness between 0 and 1/2 is considered moderately skewed. If the skewness is less than 1/2 then the distribution is fairly symmetrical.

This function returns the 1st value of the sorted population value_exp.

value_exp can be an expression of any SQL data type.

Example:

The above example would return 2, because it is the 1st value of the sorted population.

This function returns the nth value of the sorted value_exp population of n elements.

value_exp can be an expression of any SQL data type.

Example:

The above example would return 30, because it is the last (6th in this case) value in the sorted population.

This function returns the middle value of the sorted value_exp population of n elements.

value_exp can be an expression of any SQL data type.

SortMiddle will return the (n+1)/2'th value, performing integer division.

Examples:

The following example would return 2, because it is the 3th value in the sorted population ((6+1)/2 = 3.5 ~=3):

The following example would return 25, because it is the 3rd value in the population ((5+1)/2 = 3).

STDDEV returns the standard deviation of the population of numeric_exp, where numeric_exp is a sample of a larger population. STDDEVP returns the standard deviation of a whole population.

numeric_exp must be a number, or a numeric expression.

The standard deviation statistical function is used to depict dispersion among the measures of a given population.

To find the standard deviation of a population, the variance must first be defined, since the square root of the variance equals the standard deviation of the population.

To calculate the standard deviation of a sample of a population, you must first calculate the variance of the sample.

Returns the Common Trimean of the Population of numeric_exp.

numeric_exp must be a number, or a numeric expression.

The common method for calculation of the trimean is adding the 25th percentile plus twice the 50th percentile plus the 75th percentile and dividing the sum by four. The trimean is almost as resistant to extreme scores as the median and does not wobble as much from sample to sample as does the average in a skewed distribution. The trimean is a good measure of central tendency. The trimean requires more information than the median because it includes the upper and lower quartiles. The formula CONNX uses is as follows;

trimean = (quartile1 + 2*median + quartile3) / 4

Tukey's method (which used upper and lower hinge instead of the 25th percentile and the 75th percentile) produces a very similar answer. The lower hinge is the median of the lower half of the data up to and including the median. The upper hinge is the median of the upper half of the data up to and including the median. The hinges are the same as the quartiles unless the remainder when dividing the sample size by four is three.

VARIANCE returns the variance of the population of numeric_exp, where numeric_exp is a sample of a larger population. VARIANCEP returns the variance of the whole population.

numeric_exp must be a number, or a numeric expression.

The variance is used to depict the dispersion among the measures of a given population. To find the variance, you must first find the mean of the scores, find the measurement by which each score differs from the mean, find the square root of the difference, and if calculating the variance of a sample, divide the number by (n-1).

In a list of 'n' numbers, the Variance is the sum of the square of the differences between each number and the mean of the sample of the population or the whole population. Here is the formula CONNX uses when calculating the variance of a sample of a larger population. For VARIANCEP, the divider is N: