Defining size-based windows
As well as time, you can specify windows that contain only a certain number of items. In a size-based window, as each new item arrives, it is added to the window. After the number of items in the window reaches the window size limit specified in the query, the arrival of a new item causes the removal of the oldest item from the window.
The syntax for defining a size-based window is as follows:
retain windowSizeExpr
Replace windowSizeExpr with an expression that returns how many items you want to retain in the window as an integer value. For example, the following query calculates the sum of the last two items in a stream of floats:
stream <float> sums := from v in values retain 2 select sum(v.number);
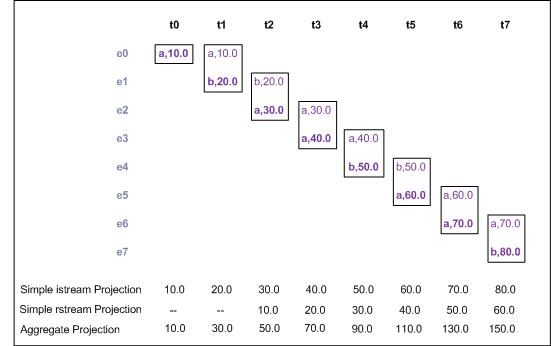
The following diagram, which uses the same notation as the previous section, illustrates how this works in practice.
The query before the diagram corresponds to the aggregate projection. The three queries shown here are:

Simple istream projection:
from v in values retain 2 select v.number

Simple rstream projection:
from v in values retain 2 select rstream v.number

Aggregate projection:
from v in values retain 2 select sum(v.number)
When an event arrives in the window, it appears in the istream of a simple, non-aggregate projection. The first item remains in the window when a second item arrives. When a third item arrives, the first item is no longer in the window and it appears on the rstream of the simple, non-aggregate projection. Likewise, when the fourth item arrives in the window, it appears in the istream and the second item appears on the rstream of the simple projection, and so on. The behavior of the aggregate projection is that whenever an item arrives in or is removed from the window, a new sum appears on the istream of the aggregate projection.