There are some cases where a measurement would be used where a numeric measurement value does not represent a continuous-time property. For example:

In contrast to the continuous-time values, each of these are significant, even if two measurements are of the same value. The time of each measurement may have some significance, but the time between subsequent measurements is of no great significance. If the measurements were received with slightly different timings, or even potentially out of order, this would not signify a difference (for example, the sum of the value of tickets does not change if they are processed in a different order or with different timings, and the time between values is unlikely to be uniform). Note that by discrete-time we are only referring to the time of the measurements. The value may still be continuous. For example, weight is a continuous value, but we may weigh individual parcels - while the weight of a parcel may be representable to fractions of a gram of weight. If we are between two parcels on a conveyor belt, there is no current value for the weight of the parcel at that point. The value could also be discrete. For example, the ticket value would typically be a discrete value (for example, to the nearest cent, or one of a few predefined ticket values).

Compare also: https://en.wikipedia.org/wiki/Discrete_time_and_continuous_time and https://en.wikipedia.org/wiki/Continuous_or_discrete_variable. In practice, all measurements are samples of a continuous-time property.

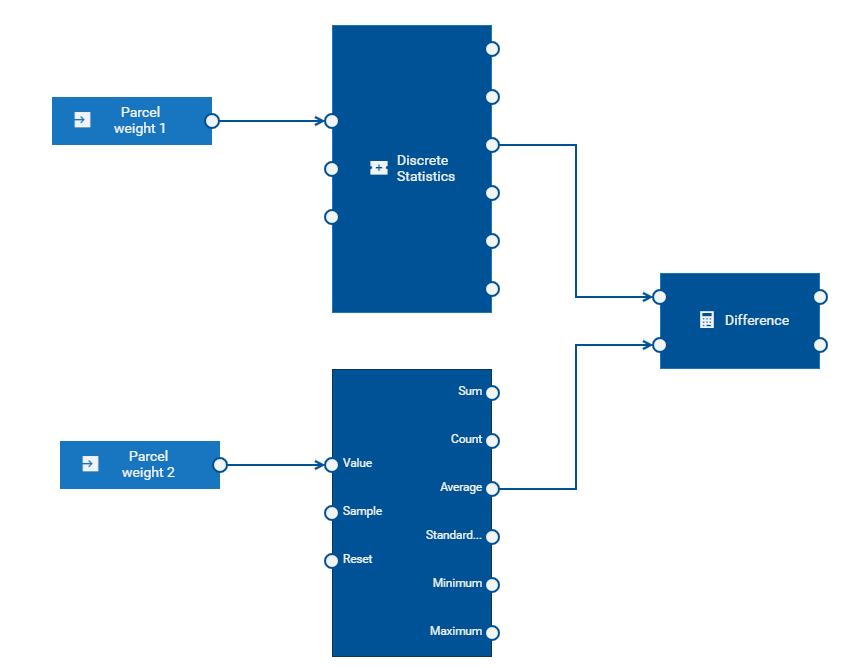
When dealing with discrete-time inputs, you should use the Discrete Statistics block rather than the Average (Mean) block. While it is possible to connect an input from a parcel weight sensor to the Average (Mean) block, the Average block weights by time. For example:

Compare this to the table in On-change inputs and time windows, looking at times 00:10 onwards (that is, what would be in a window from 00:10 to 00:20). Note that the continuous-time block would generate a different output if the inputs occurred at different times, while a block averaging values based on discrete-time would not.

Note that by default measurements are treated as continuous-time values. So it is possible, for example, to calculate the difference between two values:

The above example gives the difference between the most recent weight received by two sensors. This may not be a particularly useful distinction if these are genuinely discrete-time inputs. However, it can make sense to compare the difference of averages (or means) between two discrete-time inputs. The Average output port of the Discrete Statistics block gives a continuous-time value: