Analytics Builder 10.10.0 | Using Analytics Builder for Cumulocity IoT | Details of Values and Blocks | Values as representations of continuous-time physical quantities | On-change inputs and time windows
 
On-change inputs and time windows
If an on-change input is connected to an aggregate block such as the Average (Mean) block, then the block should treat the input as continuously having the most recent value it received. This is significant for blocks that maintain a time window. Even if the block last received an input (and thus had its $process action called) more than the time window ago, the contents of the window will contain the most recent value. For example, consider the Average (Mean) and Integral blocks with window duration set to 10 seconds, and input as so:
Time
Input value
Window contents
Output of the Average (Mean) block
Output of the Integral block
00:00
10
0: 10
10
0
00:02
11
0-2: 10
10
20
00:10
11
0-2: 10, 2-10: 11
10.8
108
00:12
11
2-12: 11
11
110
00:19
9
9-19: 11
11
110
00:20
8
10-19: 11; 19-20: 9
10.8
108
In this case, note how a measurement received at time 00:02 still has influence on the output at 00:19 and later - because it is not replaced until 00:19. Also note that when a new value occurs, it has zero influence on the average or integral - it has not been that value for any time yet. The only exception is for the Average (Mean) block when it starts - with an empty window, the output is the input value.
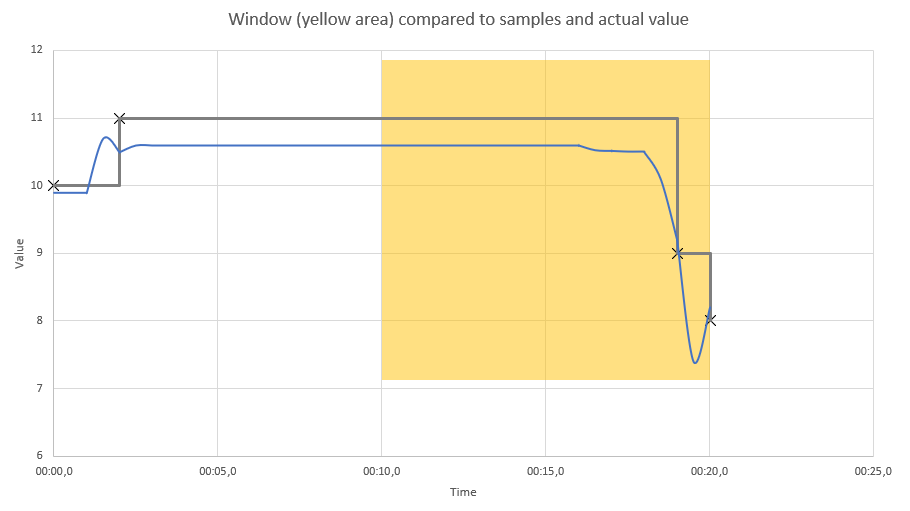
Also refer to the diagram below for what values the window covers at time 00:20:
Window compared to samples and actual value
While only the measurement updates with values 9 and 8 were received within the window, the average value within the window is close to the 11 value. The measurement update for that was received at time 00:02, but as it is a continuous value, it continues to hold the 11 value until time 00:19.
Note that for a block such as Missing Data, the absence of input for some time may affect the behavior of the block. If the Missing Data block is configured with a 10 second duration, then it would trigger at time 00:12.
If the Average (Mean) and Integral blocks receive a regular input from a regular sampling sensor, then the block will receive more measurement values, and the comparable table is:
Time
Input value
Window contents
Output of the Average (Mean) block
Output of the Integral block
00:00
10
0: 10
10
0
00:01
10
0-1: 10
10
10
00:02
11
0-2: 10
10
20
00:03
11
0-2: 10, 2-3: 11
10.333
31
00:04
11
0-2: 10, 2-4: 11
10.5
42
00:05
11
0-2: 10, 2-5: 11
10.6
53
00:06
11
0-2: 10, 2-6: 11
10.667
64
00:07
11
0-2: 10, 2-7: 11
10.714
75
00:08
11
0-2: 10, 2-8: 11
10.75
86
00:09
11
0-2: 10, 2-9: 11
10.778
97
00:10
11
0-2: 10, 2-10: 11
10.8
108
00.11
11
1-2: 10, 2-11: 11
10.9
109
00:12
11
2-12: 11
11
110
00:13
11
3-13: 11
11
110
00:14
11
4-14: 1
11
110
00:15
11
5-15: 11
11
110
00:16
11
6-16: 11
11
110
00:17
11
7-17: 11
11
110
00:18
11
8-18: 11
11
110
00:19
9
9-19: 11
11
110
00:20
8
10-19: 11; 19-20: 9
10.8
108
Note that the highlighted lines are the same as without the repeated measurements. Repeated measurements of the same value received by these blocks make no difference to what the block would calculate if re-evaluated.