Kurtosis is used in distribution analysis to describe how big the tails are for a distribution. Kurtosis indicates the likelihood of an event far away from the average. Kurtosis is based on the size of a distribution's tails. A distribution with approximately the same kurtosis as the normal distribution is called mesokurtic (meaning medium-curved). The mesokurtic kurtosis of a normal distribution is 0. If a distribution is short and flat with small tails it is described as platykurtic (flat-curved). For a platykurtic distribution, individual observations are spread out fairly uniformly across their range. If a distribution is tall and slender with relatively large tails it is spoken of as leptokurtic (slender-curved). For a leptokurtic distribution, observations tend to cluster densely about some particular point in the range.
The following formula can be used to calculate kurtosis of the sample from the raw moments:
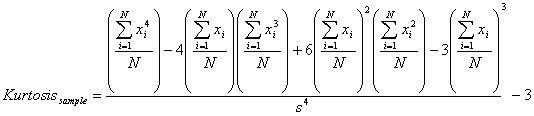
where s is the standard deviation of the sample. Subtract 3 because the kurtosis of the normal distribution is 3 (without the subtraction). By subtracting 3, the direction of the kurtosis can be seen by examining its sign. Kurtosis ranges from -2 (highly platykurtic) to 0 (mesokurtic) to +infinity (highly leptokurtic).
numeric_exp must be a number, or a numeric expression.