To discern how scattered observations are about some central value, choose either the median or the mean for the central value. If you should choose the median, average deviation from the median value is one such measure of dispersion. The average deviation (also known as the mean deviation) about the median is the average absolute difference between the observed values and the median (central value in an ordered set) for all values in the data set. For any fixed sample, choosing the median rather than some other measure of central tendency minimizes the mean deviation. Sometimes, the calculation is performed using distance from the mean instead of the median (see AVEDEVMEAN). To calculate the average deviation of the median, use the absolute value of the difference between each observation and the median. While the mean deviation is sometimes called the mean absolute deviation, this is not strictly correct unless the data is categorized into bins first. For estimating population standard deviation in a normal population, the mean deviation is not as efficient as the sample standard deviation.
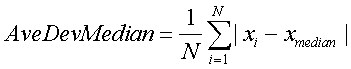
In other words, we take the sum of the absolute value of all observations minus the median and divide that sum by the number of observations (N).
numeric_exp must be a number, or a numeric expression.
Flaws exist in using this calculation. If a sample is taken and the accuracy of a process using a sample is estimated, the
result is a different estimate if the sample is divided into two smaller samples and the calculation is performed on the subsamples.
The amount of underestimation is not only a function of the sample size, but also a function of the probability of the distribution
of the errors in
measurement.
There are also some special merits in this calculation. It is not unheard of to be dealing with a distribution whose variance
does not exist. In this case, all higher moments and derivative measures such as the standard deviation are useless as a measure
of the data's width around its mean. Attempted calculations of the statistics using higher moments produce random results.
The average deviation does not suffer from this defect but is a good measure for estimation for broad distributions with a
significant number of outlier points. Higher order moments or statistics involving higher powers of the input data are less
robust than lower moments or statistics that involve only linear sums or
counting.